Reciprocal Functions

The task today was to look at a function f(x) and its reciprocal 1/f(x). We were looking for connections between the two.

The first thing I asked groups (visible random) to do was graph y = x and the reciprocal y = 1/x. When they were done I had them graph y = x^2 and the reciprocal y = 1/x^2.

Here is what it looks like.

From these two examples we were able to talk about some characteristics of f(x) and its reciprocal.

Next groups were asked to draw a cubic and its reciprocal. I encouraged students to use the new knowledge that we had discovered from the first two graphs.

 We then pulled out these connections between f(x) and its reciprocal.

 



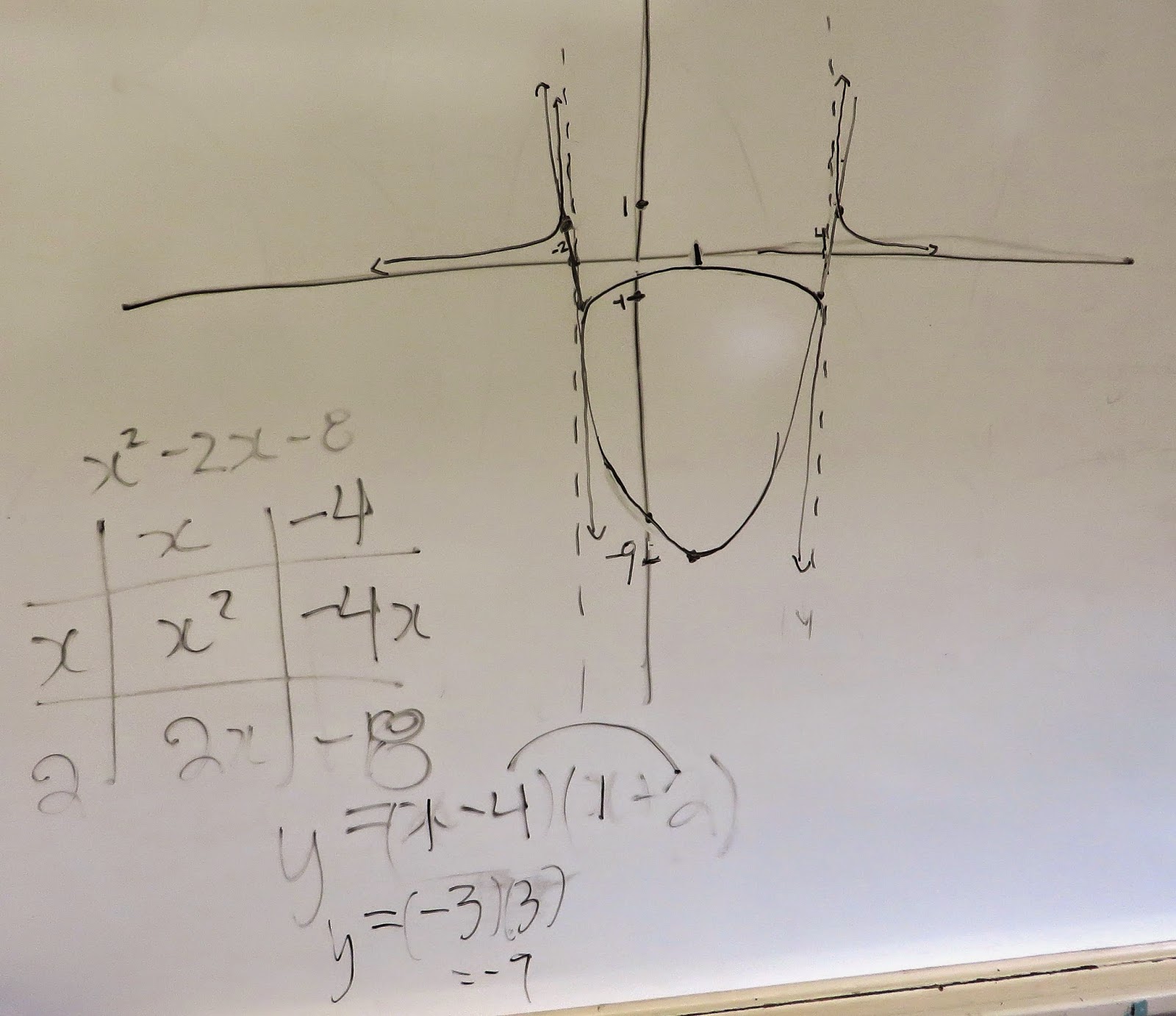
Then we tried a specific quadratic and its reciprocal. This required students to factor the quadratic and find the vertex. Okay this was the first time we had mentioned or tried factoring a quadratic. They would also need the vertex. This proved more difficult than I had expected. No worries we will be factoring soon.

Then I asked students to graph y = sin x and its reciprocal y = 1/sin x = csc x.

 

Students were then asked to graph y = cos x and its reciprocal y = 1/cos x = sec x. 

This group did both in one graph.

Lastly we looked at combining two functions to graph y = tan x = sin x / cos x. This is not an example of reciprocal functions but it is an example of a rational function. We used a table of values for sin x and cos x to create a table of values for sin x / cos x.



 

Lastly the nice thing about whiteboarding - you get to see students doodles. Layet Johnson an artist friend of mine would be proud.

Clearly not me -this guy has hair!